|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Limites du test
|
|
|
|
|
|
|
|
Corrections proposées |
De
nombreux auteurs ont proposé des indices pour estimer l’accord entre des
jugements catégoriels qui reposent pour la plupart sur le modèle suivant :
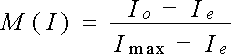
avec
I
: une statistique d’accord sur un tableau
de contingence
Io : l’accord observé
Ie : la valeur attendue sous
l’hypothèse de
l’indépendance des jugements (He)
Imax
: la valeur maximale que peut prendre I
M(I)
: une statistique d’accord corrigée de
l’accord sous He
La
principale différence entre ces indices concerne l’estimation de la
concordance aléatoire Ie.
Scott[15],
en 1955, propose l’index d’accord P
avec :
![]()
L’indice
de Scott apparaît en fait comme un cas particulier du coefficient Kappa où
l’on suppose l’égalité des marginales.
Bennet[16],
en 1954, propose un coefficient S pour lequel Ie
est toujours égale à 0,5.
Cicchetti
et Feinstein[17]
ont proposé des corrections aux limites du test Kappa, puis Byrt[18],
en 1993, présente un nouveau test PABAK
dérivé de Kappa qui équilibre les effectifs concordants et les effectifs
discordants du tableau de contingence. Finalement le test PABAK est identique à
l’index G proposé par Holley
et Guilford[19] en 1964 dans le cas d’un tableau 2´2 :
![]()
qui
peut être généralisé pour r
modalités de jugement :
![]()
Il
faut noter d’autre part, que la formulation du test Kappa multi-juges proposée
par Fleiss corrige le biais puisqu’elle fait
l’hypothèse de l’égalité des marginales.
|
|