 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Accord entre plusieurs juges
|
|
|
|
|
|
|
|
|
|
|
Cas où le nombre de jugements est constant entre les observations |
|
|
Exemple |
Nous
reprenons les résultats de notre exemple (Tableau
II) concernant l’étude d’accord entre deux tests biologiques.
Nous
utilisons la méthode générale de
calcul du coefficient Kappa qui n’impose pas un nombre constant de jugements
entre les observations, bien que dans notre exemple
=
2 puisqu’il n’y a pas de jugement manquant.
Nous
calculons tout d’abord la proportion de classement des 200 observations par
les 2 juges dans la catégorie positive, soit :
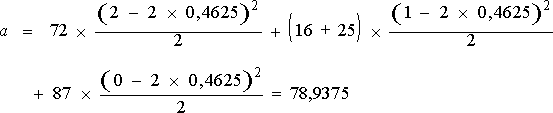
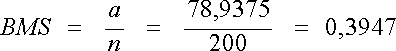
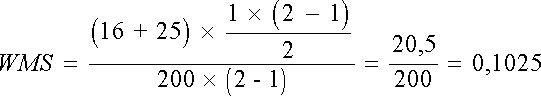
Ce
qui nous permet d’obtenir la valeur du coefficient Kappa de l’étude :
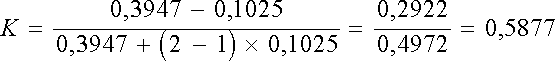
Dans
notre exemple,
=
m = 2 avec
le
nombre moyen de jugements par observation et m
le nombre de juge, ce qui permet de retrouver aisément l’expression du
coefficient Kappa de Cohen :
avec
WMS, la proportion moyenne de désaccord
d’un juge d’où la proportion de désaccord des juges qui est égale à m
´
WMS et la proportion de concordance des juges : Po
= 1 - (m ´
WMS) avec m le nombre de
juges ;
et
BMS qui représente la quantité
d’accord disponible au-delà de l’accord aléatoire moins la proportion de désaccord
due aux m - 1 juges, soit :
d’où
l’expression habituelle de Kappa :
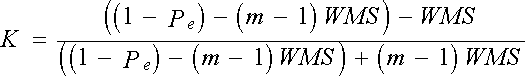
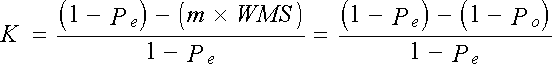
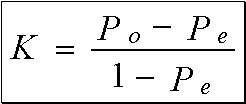
Pour
calculer le coefficient Kappa, on peut utiliser les proportions des réponses
discordantes et non plus les proportions des réponses concordantes observées Po
et aléatoires Pe. En
posant u = 1 - Po et v = 1 - Pe,
on écrit :
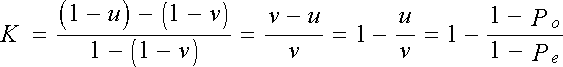
En
faisant intervenir la proportion moyenne des réponses discordantes (WMS)
et la proportion de classement des observations par les juges dans la catégorie
positive, nous retrouvons l’écriture équivalente de Kappa présentée précédemment
:
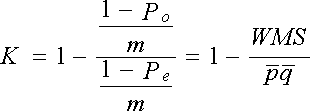
La
valeur du coefficient Kappa de notre étude est légérement sous-estimée par
les formules de Fleiss (K = 0,5877)
par rapport à celle obtenue par la formule de Cohen (K = 0,5885). Fleiss, contrairement à Cohen, suppose l’égalité
des marginales ce qui n’est pas le cas dans notre exemple puisqu’il existe
un biais entre les tests biologiques (16 et 25 réponses discordantes).
Dans
le but d’unifier les deux indices dans notre exemple, nous proposons une méthode
qui apporte la correction nécessaire aux formules de Fleiss.
Nous
calculons la somme des carrés des écarts entre les proportions de désaccord
et la proportion moyenne de désaccord, soit :
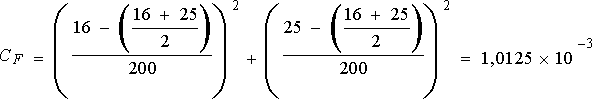
Les
biais entre les observateurs réduisent la proportion de concordance aléatoire Pe
comme nous le verrons dans le chapitre suivant. Il faut donc ajouter notre terme
correctif CF à BMS :
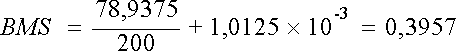
puis
nous recalculons le coefficient Kappa, soit :
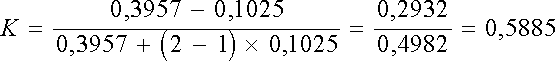
qui
est bien la valeur obtenue par la formule de Cohen.
Cette
correction peut être généralisée aux études multi-juges à deux modalités
de jugement. Par exemple, pour trois juges à réponses dichotomiques nous
devons calculer deux sommes des carrés des écarts entre les proportions de désaccord
et la proportion moyenne de désaccord : une pour le niveau de désaccord ayant
une réponse positive pour deux réponses négatives et l’autre pour le niveau
de désaccord ayant deux réponses positives pour une réponse négative.