Le Coefficient Kappa

	Introduction
	Définition de l'accord
	Accord entre 2 juges
	Accord entre plusieurs juges
	Limites du test
	Usages du test
	Applications pratiques
	Conclusion
	Annexes

Références

 

	Téléchargement
	Liens Internet
	Note de l'auteur
	Contact

Accord entre 2 juges

	Définition du coefficient Kappa
	Exemple
	Le coefficient Kappa pondéré

Certaines discordances entre les juges sont plus graves que d’autres. Cohen propose de donner à chacune des cases du tableau de contingence, un poids w_ij fixé a priori qui reflète l’importance que l’on attribue au désaccord.

Au tableau de contingence r´r représentant les résultats d’une étude d’accord, nous associons une matrice de poids r´r notée W définissant l’importance de chaque désaccord. Le tableau V défini la notation utilisée.

Tableau V - Matrice de poids W associée à un tableau de contingence r´ r

On utilise le plus souvent des poids de concordance plutôt que des poids de discordance ; ceci peuvent varier de 1 pour les cases diagonales à 0 pour les cases qui correspondent au plus grand désaccord en considérant que l’échelle des catégories de jugements est ordonnée.

Le choix des poids du Kappa pondéré K_w peut être réalisé selon un système de pondération linéaire où chaque poids se calcule d’après :

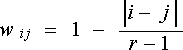
ou par un calcul de type quadratique :

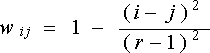
avec

         i        : la i^ème colonne de la matrice des poids

         j        : la j^ème ligne de la matrice des poids

         r        : le nombre de modalités de jugement

         w_ij     : le poids de la case ij du tableau de contingence

Remarque n°1

La matrice des poids sera choisie symétrique dans le cas d’une étude de reproductibilité et pour d’autres types d’étude elle peut être choisie asymétrique si l’on désire souligner une dissymétrie entre les juges.

Prenons par exemple la situation d’apprentissage d’un étudiant A pour lequel on désire évaluer la conformité de ces jugements à ceux d’un expert B dans le domaine considéré. Deux modalités de jugement sont proposées (+ et -) et nous considérons en outre que le désaccord «A+ B-» est plus grave par ces conséquences que le désaccord «A- B+». Dans ces conditions, il est possible d’associer au tableau de contingence 2´2 une matrice asymétrique de poids de concordance qui pourrait être de la forme :

Remarque n°2

Peu de travaux portent sur la façon dont on doit définir le système de poids et l’approche la plus logique semble être la définition du système par consensus entre experts.

 La concordance observée P_o(w) du kappa pondéré en fonction de la matrice des poids de concordance est définie par :

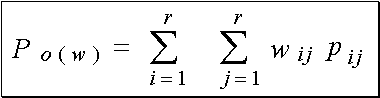
et la concordance aléatoire P_e(w) est :

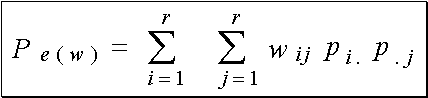
 avec

         p_ij = n_ij / n

         p_i. = n_i. / n

         p_.j = n_.j / n

         n étant le nombre total d’observations

Le Kappa pondéré est donné par :

Remarque n°3

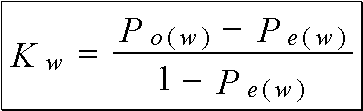
Les formules exprimant le Kappa non pondéré sont une simplification des formules du Kappa pondéré. En effet, K est un cas particulier de K_w avec le système de pondération : w_ij = 1 " i = j et w_ij = 0 " i ¹ j.

Signification statistique

Pour tout savoir ou presque sur le test statistique Kappa...